ID3

Árvores de Decisão

O primeiro tópico a ser abordado aqui no blog são as árvores de decisão, sendo os mais conhecidos o algoritmo ID3 e no seu sucessor C4.5. Iremos implementar primeiramente a versão mais básica (ID3) e depois de pronto o modificaremos para que se torne o seu sucessor.

O nosso algoritmo básico constrói as árvores de decisão de uma forma top-down (de cima para baixo), fazendo uma simples pergunta: "Qual atributo deve ser usado?". Para responder isso cada atributo é testado usando um método estatístico para determinar o ganho de informação que aquele atributo gera na hora de classificar a nossa base de treinamento. Após a seleção esse atributo vira o topo da árvore e cada valor que esse atributo pode assumir vira uma folha e a base de dados é separada de acordo, o processo todo é repetido para cada folha, usando apenas os exemplos associados a ela. Iremos usar a implementação greedy desse algoritmo, pois ele nunca volta atrás para reconsiderar as escolhas feitas anteriormente.

Para a implementação de uma árvore de decisão que aceite apenas valores booleanos como saída, teremos o seguinte pseudocódigo:

IDE3 (Exemplos, atribuito_classificador, Atributos)

• Criar a folha inicial da árvore Root
• Se todos os objetos são positivos em Exemplos, retornar uma única folha com a saída verdadeira.
• Se todos os objetos são negativos em Exemplos, retornar uma única folha com a saída false.
• Se Atributos estiver vazio retornar uma única folha com a saída mais comum na base.
• Caso contrário faça:
• A recebe o atributo de Atributos que melhor classifica Exemplos.
• Root recebe A
• Para cada possível valor v de A teremos:
• Adicionar uma nova folha a A com o valor correspondente a v.
• Sendo X o resultado de Exemplos com os objetos que contenham v como atributo.

• Se o X gerado for vazio:
• Adicionar uma folha a Root com o valor mais comum da base.
• Caso contrário:
• ID3 (X, atribuito_classificador, Atributos – A).

• Término.
• Retorne Root.

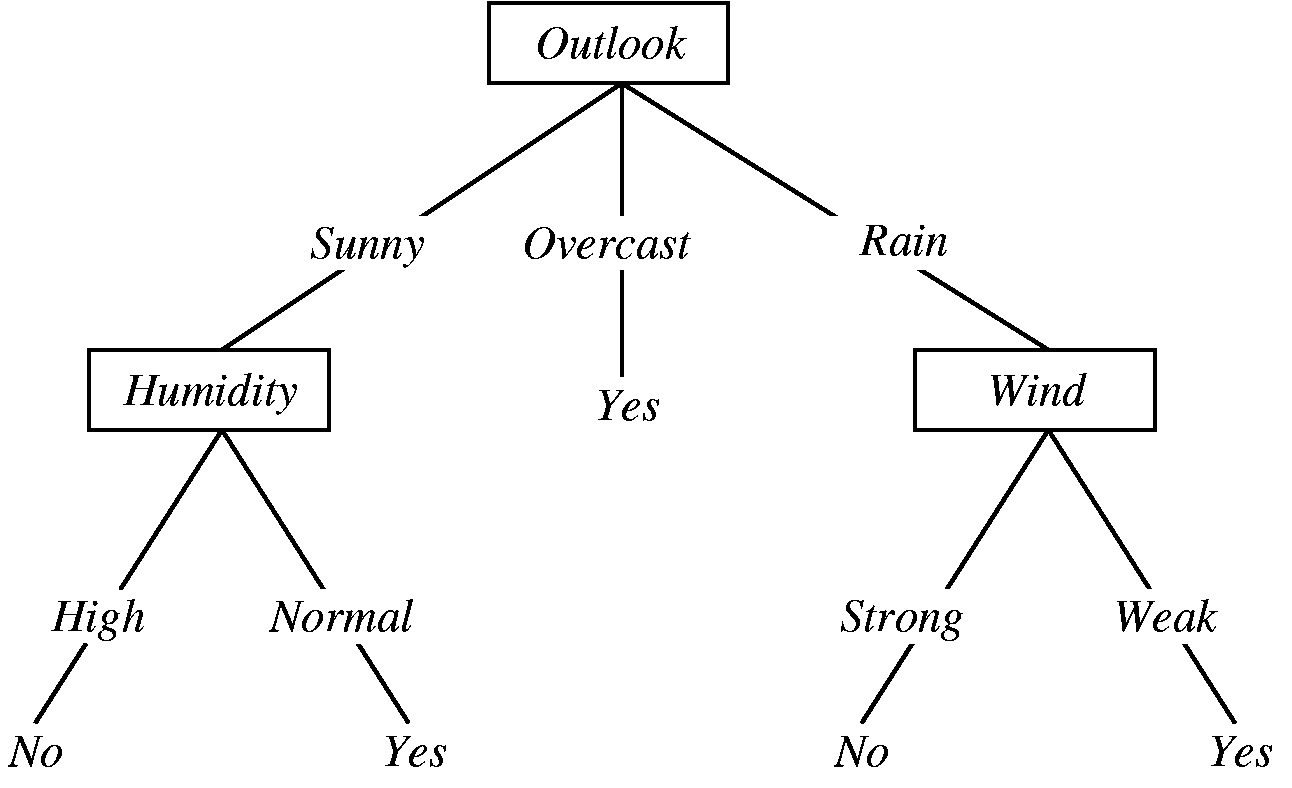
Para medir qual atributo melhor classifica a base de dados vamos utilizar o cálculo de ganho de informação, você pode conferir uma descrição completa da equação nesse link.

Como todos algoritmos o ID3 possuí algumas limitações e capacidades, vamos ver abaixo algumas delas:

• O ID3 na sua forma inicial, e a que será implementada, não possui nenhuma forma de backtracking, portanto está sujeito a convergir para soluções ótimas locais. No caso do ID3, uma solução ótima local corresponde ao único caminho considerado pelo algoritmo.
• ID3 usa todos os exemplos do conjunto de treinamento a cada iteração, não importando o nível em que a árvore se encontra. Essa característica faz com que o ID3 seja muito menos suscetível a erros no conjunto de treinamento.
• O ID3 mantém apenas uma única solução, o que faz com que ele não seja capaz de otimizar os resultados obtidos.

Para encerrar esse post podemos ver abaixo um exemplo de resultado obtido com o ID3: